Tại sao lại
như vậy? Vì qua quá nhiều lần gặp trong quá trình biến đổi tích phân. Bản thân
tôi nhận thấy như vậy và nhất là trong những kỳ thi tuyển sinh đại học gần đây
có xu hướng càng dễ. Khi đó nó sẽ hướng về những tích phân hàm hữu tỉ đơn
thuần.
Trước đây,
tích phân có rất nhiều dạng cần phải biến đổi từ nhiều bài toán hay. Nhưng
trong kỳ tuyển sinh đại học 2014 vừa rồi ở khối B lại đưa cho chúng ta một câu
tích phân hữu tỉ chỉ đơn thuần. Việc tính toán nó không gì có thể dễ dàng hơn.
Có thể nói nó dễ nhất trong những đề thi tuyển sinh đại học từ trước đến nay.
Cũng nhắc
lại, tích phân hữu tỉ là loại tích phân của hàm phân thức sơ cấp. Nghĩa là tích
phân của những hàm số phân số mà tử và mẫu của nó là những hàm số sơ cấp(Bậc
một, bậc hai, bậc ba…). Mà không có sự xuất hiện của những hàm số siêu việt(bao
gồm hàm mũ, lô-ga-rít, lượng giác). Do đó việc tính những tích phân loại này
được xem như khá đơn giản. Trước khi tính toán bước tiếp theo thì bước đầu tiên
ta phải quan sát và so sánh bậc của tử và bậc của mẫu. Nếu bậc của tử lớn hơn
hoặc bằng bậc của mẫu thì ta tiến hành chia đa thức để được một phân thức.
Trong đó có bậc của tử nhỏ hơn bậc của mẫu.
Nó sẽ đưa
cho chúng ta một phân số thỏa mãn điều kiện trên với mẫu chỉ là nhị thức bậc
nhất hoặc tam thức bậc hai thuần túy.
Đối với mẫu là nhị thức bậc nhất thì ta
chỉ việc áp dụng ngay công thức tích phân mở rộng
Nếu mẫu là tam
thức bậc hai thì ta cũng thực hiện chia thành ba trường hợp. Tam thức bậc hai
có hai nghiệm phân biệt, Tam thức bậc hai có nghiệm kép và Tam thức bậc hai vô
nghiệm.
Đối với mẫu
là tam thức bậc hai có hai nghiệm ta thực hiện đồng nhất thức. Mà trên
Xuctu.com và trên những Video tutorial của thầy trên kênh http://www.youtube.com/user/quoctuansp
đã thực hiện khá đầy đủ loại này.
Còn đối với
mẫu là tam thức bậc hai có nghiệm kép thì ta đưa nó về loại tích phân
Cuối cùng
đối với mẫu là tam thức bậc hai vô nghiệm thì ta tiến hành đưa nó thành tích phần
hàm lượng giác. Nhưng dạng này rất hiếm gặp trong 10 năm gần đây. Thầy sẽ thực
hiện một bài đăng riêng ở sau này.
Trên đó là
những phương pháp để tính tích phân đơn giản loại này mà thầy nhắc lại cho tất
cả chúng ta để tính tích phân hữu tỉ. Quay trở lại tại sao loại tích phân này
lại quan trong đến như vậy.
Tất nhiên
kỳ thi tuyển sinh đại học cho khối D, Cao đẳng và tốt nghệp trung học phổ
thông. Nếu ra loại này thì chỉ dừng ngang ở mức độ này thôi. Chớ không hơn
nhiều lắm đâu. Nhưng đối với những kỳ thi tuyển sinh đại học các khối A, B thì
trông có vẽ chúng ta phải biến đổi chút ít cho phù hợp. Và cuối cùng đa phần
cũng phải quy về loại toán tích phân hữu tỉ này.
Tích phân
hàm số vô tỉ (hàm có chứa căn thức), tích phân đổi biến chúng ta cũng phải đưa
về tích phân hàm hữu tỉ.
Chẳng hạn: Trích từ đề thi tuyển sinh Đại học khối B-2012
Trích từ đề thi tuyển sinh Đại học khối A-2004
Trích từ đề thi tuyển sinh Đại học khối A-2003
Lời
kết: Trên đây
là những dẫn chứng để chúng ta có thể thấy được tầm quan trọng của tích phân
hàm hữu tỉ. Nhất là trong tình trạng đề thi tuyển sinh đại học càng ngày càng
hướng vào loại tích phân đơn giản này. Tất nhiên đối với những bài toán khó hơn
chúng ta phải biết cách kết hợp những loại khác nhau để giải tích phân. Nó giúp
các em học sinh thấy được vài phần để luyện thi tốt hơn trong kỳ tuyển sinh đại
học 2015 này.
Chúc các em
may mắn và thành công trong học tập.

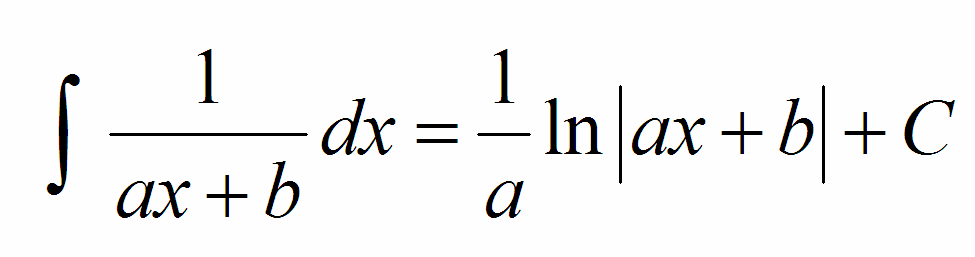




No comments:
Post a Comment