Hệ phương
trình là một mãng toán không thể tách rời trong chương trình toán trung học phổ
thông. Mà lớp 9 là nền tảng đầu tiên cho việc tiếp cận hệ phương trình. Tuy nó
đang trong giai đoạn đơn sơ nhất. Nhưng nó lại giúp chúng ta hình dung được hệ phương
trình là gì và các giải như thế nào. Để phục vụ cho điều này, chúng tôi tổng
hợp các phương pháp chính được sử dụng trong khi giải hệ phương trình loại này.
Dạng 1: Giải hệ phương trình bằng phương pháp thế
+ Từ các hệ số của phương trình (1) hoặc phương trình (2) của hệ
phương trình. Ta rút x theo y hoặc y theo x. Rồi thay vào phương trình còn lại
của hệ phương trình ta được một phương trình mới là phương trình bậc nhất một
ẩn. Giải ẩn này, rồi thay ẩn mới giải được vào phương trình ban đầu của hệ
phương trình để giải ẩn còn lại.
Một số lưu ý khi giải hệ phương trình bậc nhất hai ẩn số
+ Khi rút x theo y hay y theo x của phương trình của hệ phương
trình ta rút sao cho hệ số của nó chẳng nhất để tránh trường hợp rắc rối sau
này.
+ Kinh nghiệm cho thấy ta nên rút hệ số nào bằng một để đơn giản
nhất.
+ Khi giải hệ phương trình
bậc nhất hai ẩn số mà đề bài không yêu cầu chúng ta giải bằng phương pháp nào
thì ta thấy phương pháp nào là lợi thế của mình thì giải theo phương pháp đó.
+ Trong chương trình toán lớp 9. Người ta không cho phép sử dụng
máy tính bỏ túi để giai trực tiếp về hệ phương trình bậc nhất hai ẩn số. Tuy
nhiên, sau khi giải ta vẫn có thể dùng nó để kiểm tra kết quả một cách chính
xác. Tránh trường hợp những mắc lỗi sau này.
Ta thực hiện ví dụ sau: Giải hệ phương trình:
Dạng
2: Giải hệ phương trình bằng phương pháp cộng đại số
Từ các hệ số của phương trình (1) hoặc phương trình (2)
của hệ phương trình. Ta dùng các phép biến đổi tương đương để có được hệ phương
trình mới có các hệ số mang x hoặc mang y bằng hoặc đối nhau.
- Khi các hệ số bằng nhau ta tiến hành trừ hai phương
trình của hệ phương trình cho nhau ta được một hệ phương trình mới tương đương
với hệ phương trình đã cho. Từ đó giải tiếp để tìm nghiệm của hệ phương trình
- Khi các hệ số đối nhau ta tiến hành cộng hai phương
trình của hệ phương trình cho nhau ta được một hệ phương trình mới tương đương
với hệ phương trình đã cho. Từ đó giải tiếp để tìm nghiệm của hệ phương trình.
Ta thực hiện ví dụ sau:
Chú ý:
1. Khi đề bài không yêu cầu giải bằng
phương pháp gì thì ta có thể dùng phương pháp thế hoặc phương pháp cộng đại số
để giải. Chúng ta có thể chọn sao cho phù hợp và dễ tính toán nhất có thể.
2. Đề bài yêu cầu chúng ta không sử
dụng máy tính để giải những hệ phương trình đơn giản. Nhưng chúng ta vẫn có thể
sử dụng nó để kiểm tra kết quả. Như vậy sẽ đối chiếu lại kết quả tốt hơn.
3. Khi thấy trong các hệ số chứa x,
hoặc y là 1 hoặc -1 thì có thể giải hệ phương trình bằng phương pháp thế tở ra
tối ưu. Ngược lại, tất cả các hệ số chưa x hoặc y đều khác 1 và -1 thì giải hệ
phương trình bằng phương pháp cộng đại số tỏ ra vượt trội hơn.
Dạng 3: Giải hệ phương trình bằng phương pháp đồ thị hàm số
+ Với nhận xét
rằng: Trong phương trình (1) và phương trình (2) của hệ phương trình ta rút y
theo x được hệ phương trình.
+ Khi đó ta có
được (1) và (2) là hai hàm số bậc nhất. Mà đồ thị của hàm số bậc nhất trong hệ
trục tọa độ Oxy là một đường thẳng. Do đó, nghiệm của hệ phương trình là tọa độ
giao điểm của hai đồ thị hàm số (1) và (2).
Một số lưu ý khi
giải hệ phương trình bậc nhất hai ẩn số theo phương pháp dùng đồ thị
+ Phương pháp này
yêu cầu các em có kỹ năng vẽ hình. Cụ thể là vẽ đồ thị của hàm số bậc nhất, nên
nhất thiết các em phải có kiến thức về loại toán này.
+ Việc xác định
chính xác tọa độ giao điểm của hai đường thẳng trên hệ trục tọa độ là một việc
chỉ mang tính tương đối. Do đó, phương pháp này không cho thấy được tính tổng
quát của nó.
+ Nếu đề bài
không yêu cầu giải hệ phương trình bằng phương pháp này thì thầy khuyên chúng
ta nên giải bằng 2 phương pháp trên để có được tính chính xác cao hơn.
+ Dạng toán này,
ta đã gặp ở phần đồ thị của hàm số bậc nhất vào phần sự tương giao của đồ thị
hàm số bậc nhất.
+ Loại toán này
phát huy tác dụng khi chúng ta học chương trình toán lớp 10 sau này và các loại
toán mang tính chất nâng cao.
+ Hơn nữa, khi
biết kết hợp phương pháp giải hệ phương trình bằng phương pháp đồ thị ta có thể
áp dụng các bài toán cao hơn. Trong đó có các phương pháp tính diện tích, chu
vi …
Lời kết: Đây là ba phương pháp chính mà chúng tôi đã tổng hợp lại trong tài liệu này. Hy vọng bài đăng có thể giúp chúng ta có thể giải quyết được những bước đầu tiên về giải hệ. Tất nhiên ở các chương trình học toán về hệ phương trình sau này. Chúng tôi sẽ trình bài ở bài đăng khác.
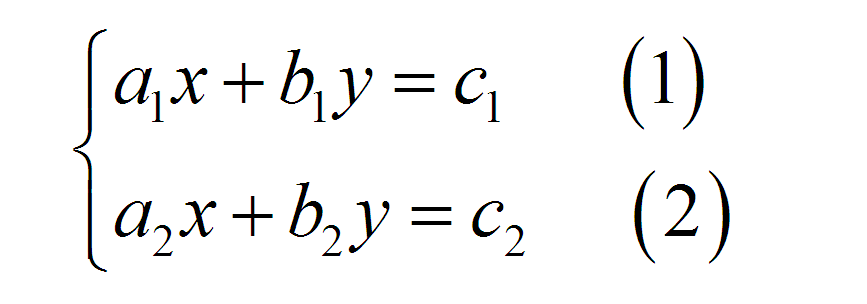




No comments:
Post a Comment